| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 빅테크
- 반도체 #tsmc #일본반도체정책 #대만일본협력 #기술격차 #문화충돌 #경제안보 #공급망 #국제협력 #산업정책
- 독서
- 3급공채
- w를찾아서
- 삼성전자
- 프리다이빙입문
- MOSFET
- 일본#후쿠시마#오염수#방류#방사선#방사능#오염#피폭#발암물질#해산물#논란#뉴스
- 닉슬립
- ai서버
- 반도체
- 자카리아
- 프리다이버
- freediving
- the money book
- 반도체란
- 사진
- 트랜지스터
- 수학#통계#몬테카를로#montecarlo#확률#과학
- 더머니북
- 입주전시공
- 노마드투자자
- 반도체기초
- 취미
- 파이썬
- brownian
- 책
- 프리다이빙
- 직장인
Archives
- Today
- Total
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 빅테크
- 반도체 #tsmc #일본반도체정책 #대만일본협력 #기술격차 #문화충돌 #경제안보 #공급망 #국제협력 #산업정책
- 독서
- 3급공채
- w를찾아서
- 삼성전자
- 프리다이빙입문
- MOSFET
- 일본#후쿠시마#오염수#방류#방사선#방사능#오염#피폭#발암물질#해산물#논란#뉴스
- 닉슬립
- ai서버
- 반도체
- 자카리아
- 프리다이버
- freediving
- the money book
- 반도체란
- 사진
- 트랜지스터
- 수학#통계#몬테카를로#montecarlo#확률#과학
- 더머니북
- 입주전시공
- 노마드투자자
- 반도체기초
- 취미
- 파이썬
- brownian
- 책
- 프리다이빙
- 직장인
Archives
- Today
- Total
sean's archive
브라운 운동(Brownian motion) - 공기 중 먼지에서부터 주식까지 본문
반응형
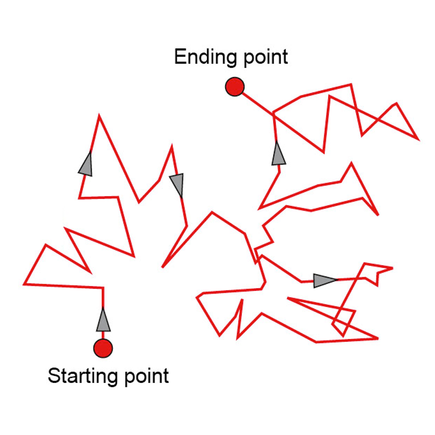
1.랜덤한 운동
- 공기 중에 떠다니는 먼지, 물에 떠다니는 가루들, 특별한 사건이 없을 때 주가의 움직임 등등.. 세상에는 랜덤한 것으로 보이는 움직임들이 있습니다.
- 이런 입자(혹은 다른 것)의 움직임은 말 그대로 자기 마음대로 (랜덤) 이기 때문에 어떤 규칙도 없을까요?
- 아니요. 그렇지 않습니다. 불규칙한 움직임들 (stochastic) 도 물리적으로 분석이 되었는데 이를 브라운 운동(Brownian motion)이라고 합니다.
- 영어로는 브라우니안 모션 인데 갈색이나 또는 음식 브라우니와는 전혀 관련이 없고 로버트 브라운이라는 과학자가 밝혀낸 표류하는 입자에 대한 서술입니다.
2. 상황 가정
- 상황을 하나 가정해 봅시다. 위, 아래, 양옆으로 랜덤으로 움직이는 어떤 입자 (가루, 먼지 등등 어떤 것이라도) 가 있다고 합시다.
- 이런 입자들이 한 번에 0에서 1까지의 거리를 랜덤하게 움직일 수 있고, 방향도 360도 랜덤이라고 합시다.
- 맨 처음에 0에서 시작해서, 1초가 지날 때마다 한 번씩 움직인다고 합시다. (편의상 초 단위를 가정, 실제로는 iteration)
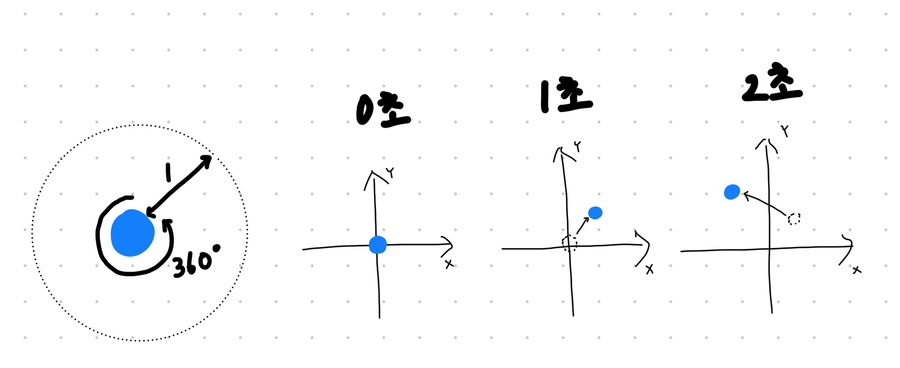
- 그렇다면 어차피 랜덤하게 움직이니까, 시간이 오래 지나도 그 자리에 그대로 있을까요? 생각해 보면 멀리 가지는 못할 것 같습니다.
- 랜덤한 운동은 실제로는 여러 입자 간 충돌로 이루어지게 됩니다. 공기 중에 떠 있는 먼지를 생각해 보면, 공기 분자와의 충돌, 크고 작은 먼지와의 충돌 등이 끊임없이 일어나게 되죠.
- 그런데 이것들도 다 랜덤이라서, 충돌을 따로 구분할 필요 없이 랜덤 한 위치의 변화로 한 번에 퉁쳤습니다. 어차피 결과는 거의 똑같을 거거든요.
- 계속 상상만 하는 것보다는 실제로 보는 게 좋죠. 간단하게 코딩을 통해 시뮬레이션을 해보았습니다.
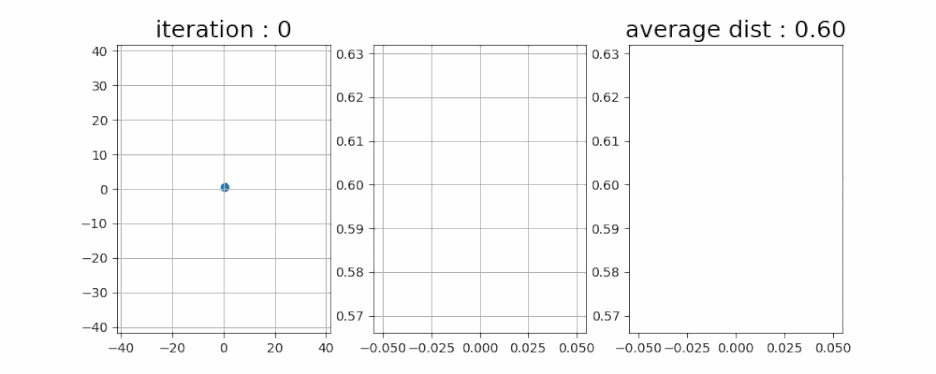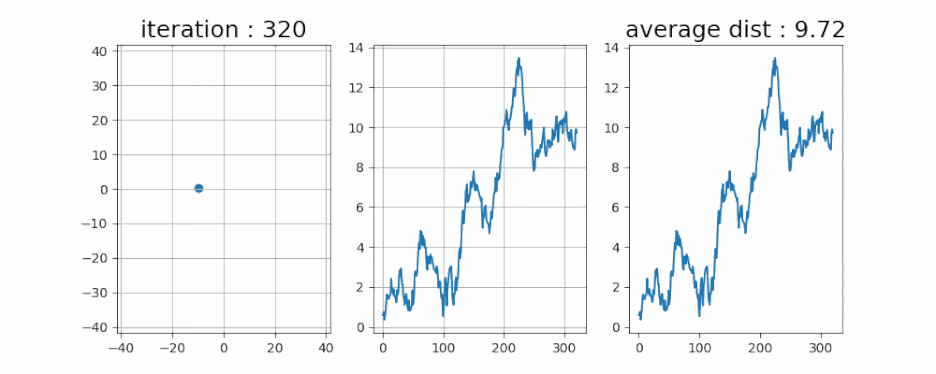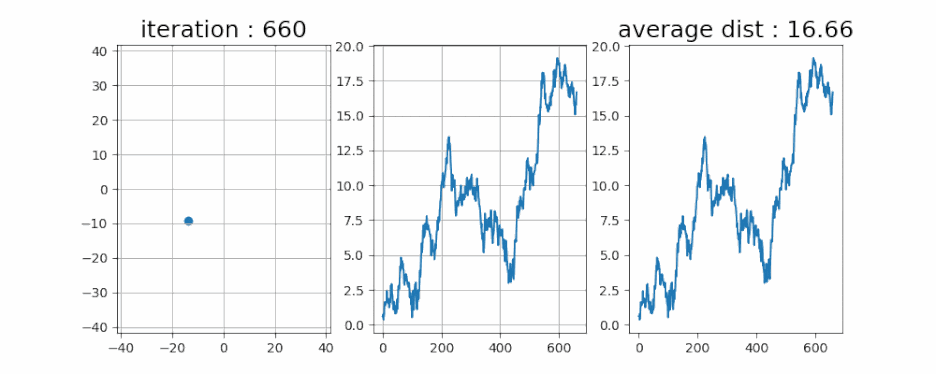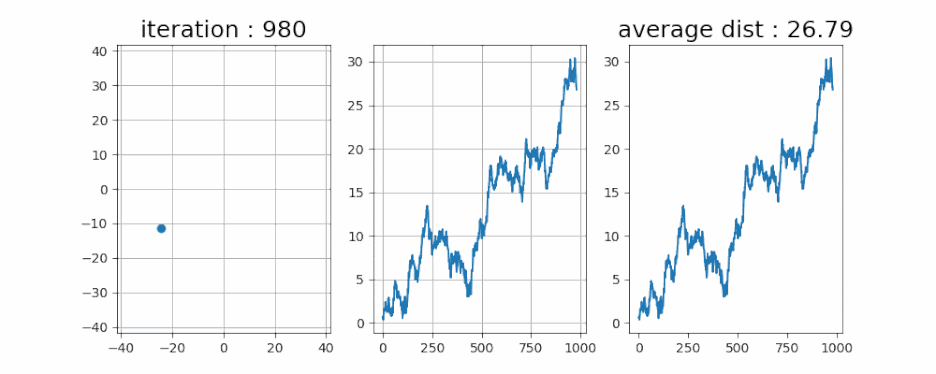
- 쉴 새 없이 움직이는 것을 볼 수 있습니다. 그런데 점점 중앙에서 멀어지는 모습을 보여줍니다. 이것도 그냥 랜덤이라서, 멀어질 수도 있고 가까워질 수도 있는데 우연히 멀어지는 입자를 관측한 걸까요?
- 그렇다면 입자 한 개가 아니라 다섯 개를 시뮬레이션 해보겠습니다.

- 다섯 개의 평균치를 해봤을 때도 점점 멀어지는 것으로 보입니다.
- 네, 랜덤으로 운동하는 입자는 그 자리에서 가만히 있지 않고, 처음 위치에서 점점 멀어지는 운동을 합니다.
- 간단하게 생각해 봅시다. 먼저 입자가 한번 움직였을 때 처음 위치와는 다른 위치로 움직이게 됩니다. 그럼 두 번째 움직일 때 처음 위치로 그대로 돌아갈 확률은 어떻게 될까요?
- 처음 위치로 돌아갈 확률은 없습니다.
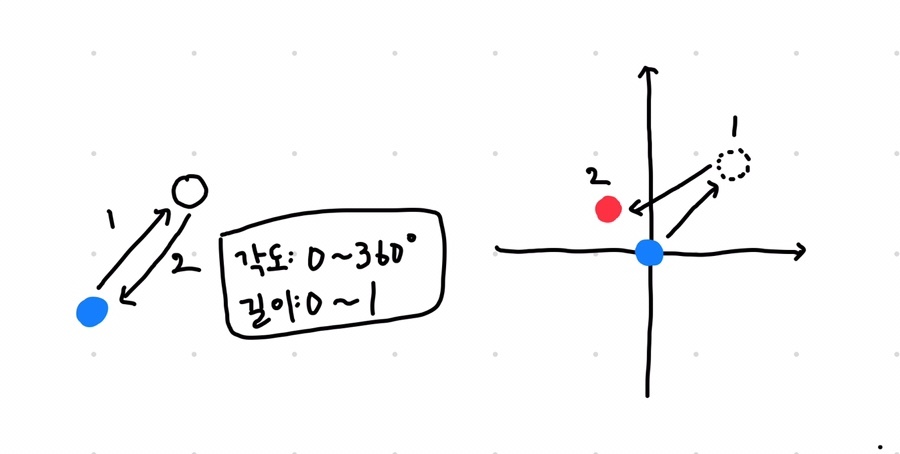
- 처음 위치로 돌아가기 위해서는 각도와 길이가 정확히 맞아떨어져야 합니다.
- 잠깐 확률적인 얘기로 들어가 보면, 0에서 1까지 사이의 숫자 중에 0.5 가 나올 확률이 몇일까요? 답은 0입니다. 0과 1 사이에 무수하게 많은 숫자가 있기 때문입니다.
- 하지만 0.5~0.6의 숫자가 나올 확률은 구할 수 있습니다. 10% 이지요. 그래서 개별 값이 나올 확률보다는 범위의 확률을 주로 사용합니다. (연속분포일 경우)
- 즉 입자는 한번 이동할 때마다, 처음 위치와는 아주 조금이라도 다른 곳에 있고 그 거리가 조금씩 누적될 때마다 처음 위치에서 더욱더 멀어지는 것입니다.
3. Brownian 운동
- 자세한 유도 식은 위키피디아에 나와 있습니다. 식을 유도하는 과정은 스킵하도록 하겠습니다. (https://en.wikipedia.org/wiki/Brownian_motion)
- 결론을 말씀드리자면 평균 이동 거리는 시간의 제곱근에 비례합니다. 100 초동안 약 10의 거리를 이동하고, 10000초 동안 약 100의 거리를 이동한다고 생각하시면 됩니다. 물론 정확한 거리는 물질과 조건에 따라 다르겠지만요.
- 처음 위치에서 멀어지긴 하지만, 멀어지는 변화량이 점점 작아지는 모양입니다.

- 정말로 그런지 알아봤습니다. 이번에는 무려 1만 개의 입자들을 움직여 보았습니다. 제일 오른쪽 그래프인 평균 이동 거리를 한번 볼까요?
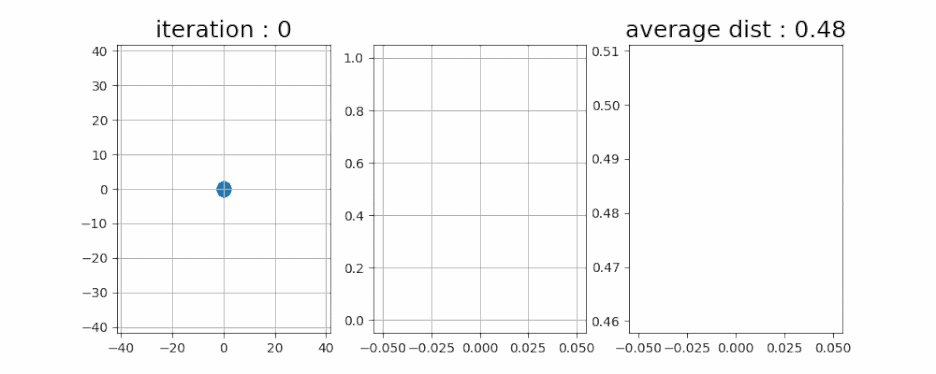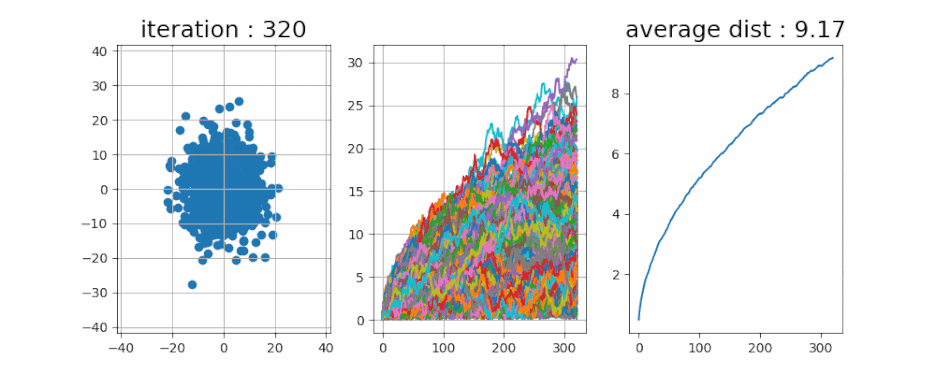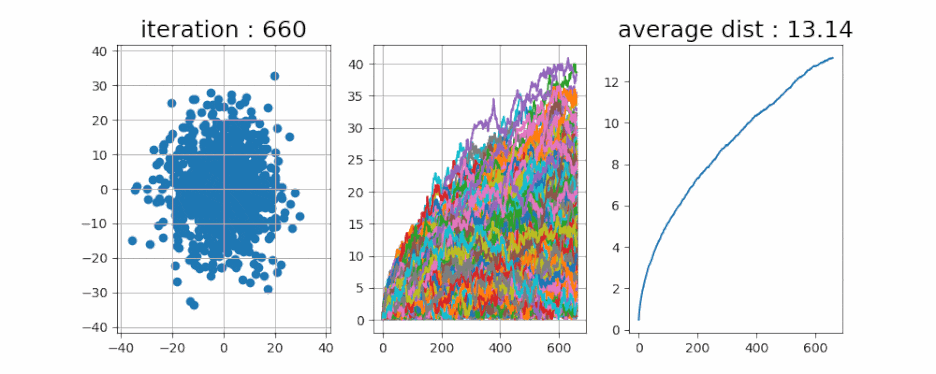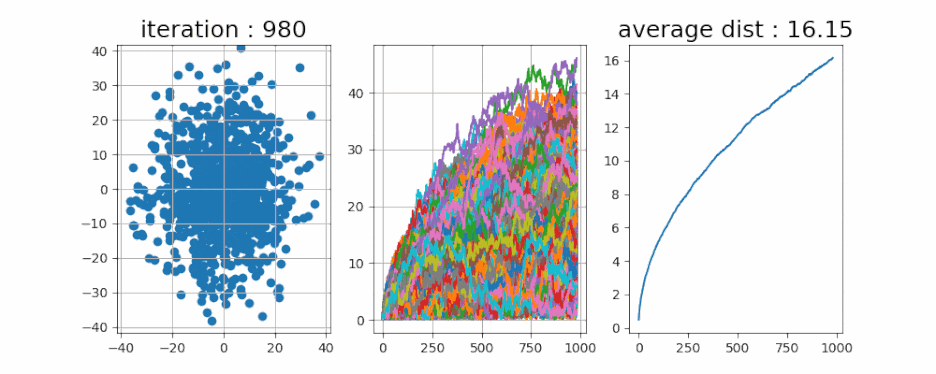
- 위에 있던 t의 제곱근 모양과 매우 흡사합니다. 1만 초동안 거리를 측정해 보면 모양이 똑같은 것을 알 수 있습니다.
- 식에 넣어보면, 제가 단순하게 랜덤 함수로 코딩했던 입자의 상수 D 값은 대략 50이라는 것을 알 수 있겠네요.
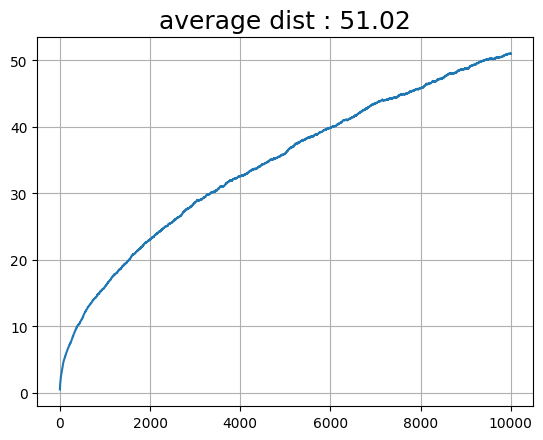
- 결국 랜덤 한 입자도 평균적으로 봤을 때는 어딘가로 계속 움직이고 있다는 뜻입니다.
4. 금융수학 - 주식과의 관계
- 그런데 브라운 모션에 대해서 글을 쓰다 보니 흥미로운 주제를 하나 발견했습니다. 앞에 얘기했지만 주식의 움직임도 브라운 모션으로 기술할 수 있더군요.
- 간단하게 생각해 보겠습니다. 수십수백만에 달하는 사람들이 각자 다른 매매 성향을 가지고 주식을 사고팔고 있습니다. 위에서 봤던 입자를 사람 한 명이라고 생각하면 됩니다.
- 그리고 외부의 요인 (알 수 있는 호재와 악재) 은 이미 개별 사람들의 행동에 반영되어 있습니다. (알거나 혹은 모르거나)
- 처음에는 랜덤하게 움직이는 것 같지만 충분히 시간이 흐르고 나면 개인의 성향에 따라, 위치가 달라져 있는 것을 알 수 있습니다. 매매를 하다 보면 수익도 나고 손해도 나고, 단타를 치는 날도 있고 장기투자(존버) 를 하는 날도 있겠지요.
- 이번엔 수익과 손해로만 그래프를 그려볼까요? 0 기준으로 위로 갈수록 수익이고 아래로 갈수록 손해라고 해봅시다.
- 그런데 아까 평균 이동거리는 점점 증가한다고 했죠? 개인의 성향이 어떻든 간에 총 평균으로 봤을 때에는 중심에서 조금씩 멀어지는 경향성을 가지고 있습니다. 이는 모든 사람의 매매량이 조금씩 증가한다는 거고 이게 증권사가 수수료로 돈을 버는 방식입니다.
- 이번엔 10만 명으로 한번 테스트를 해보겠습니다. 그리고, 모든 사람들의 수익을 평균해 보면 어떨까요?
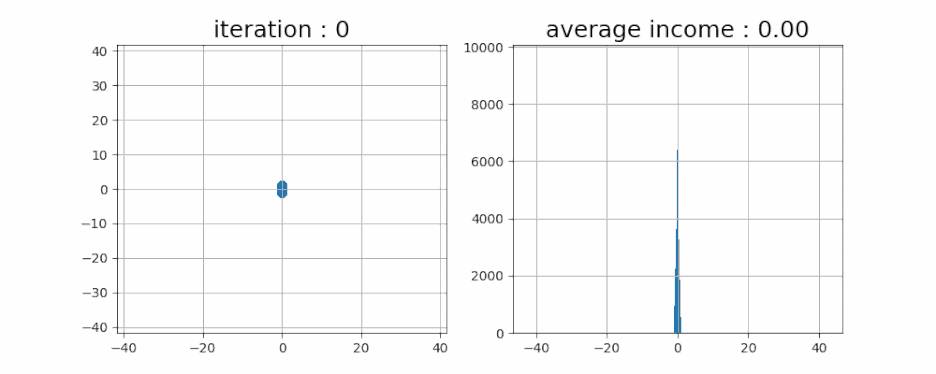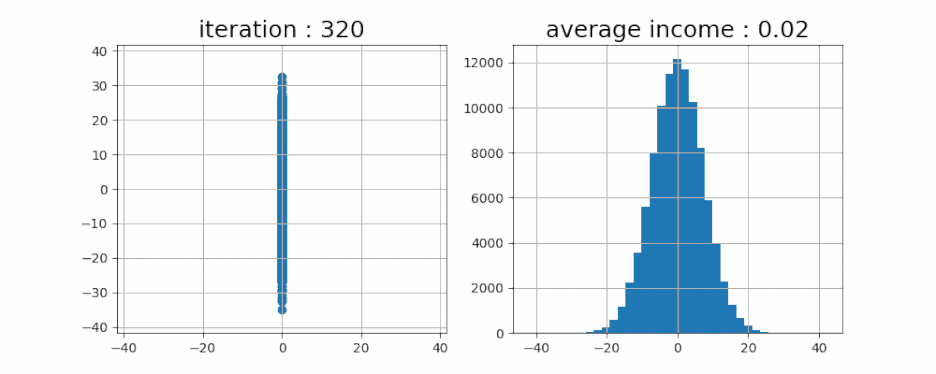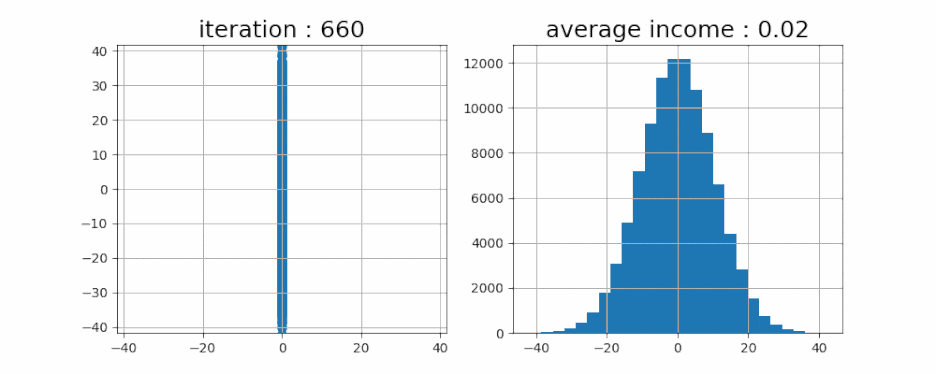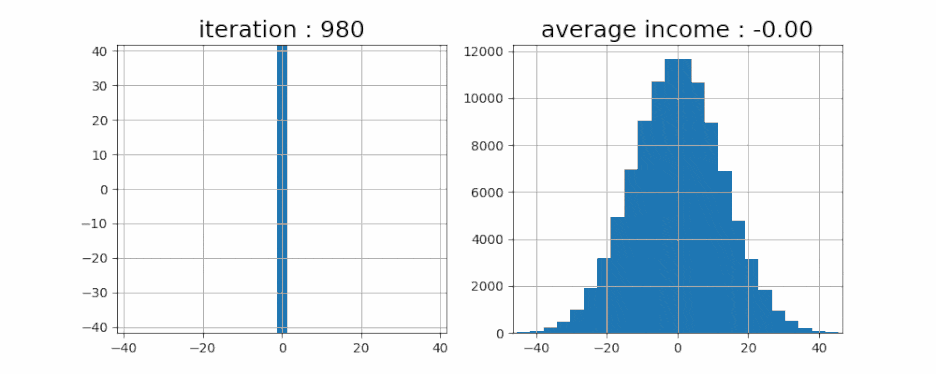
- 결과는 예상했던 0입니다. 그리고 이 분포는 정규분포를 따르죠. 물론 여기에 실제 주식 종목에 따라 약간의 랜덤이 아닌 요소를 더해주면, 분포도가 꽤 달라질 것 입니다.
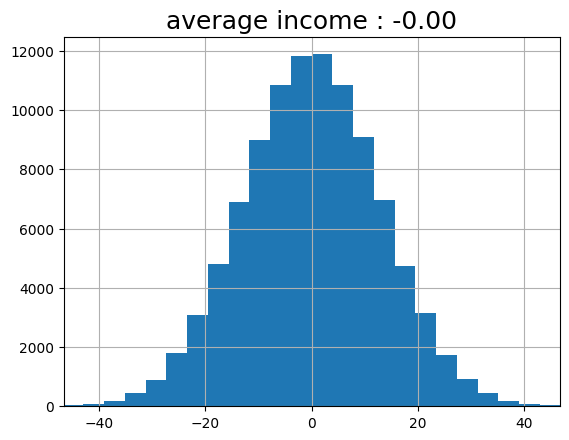
- 분포를 안다는 것은, 며칠 뒤의 가격을 예측할 수 있다는 것입니다. 브라운 운동을 통해 옵션의 가격을 계산할 수 있는데 이를 블랙-숄츠 모델(Black-Scholes Model)이라고 합니다.
- 옵션이라는 것은 예를 들면 지금 100원인 주식을 110원에 살(팔) 수 있는 권리를 뜻합니다. 대략 금융계에 큰 영향을 끼쳤다 정도만 알고 가시면 됩니다.
5. 결론
- 랜덤하게 움직이는 입자들이 움직이는 것을 브라운 운동이라고 합니다.
- 제자리에서 크게 못 벗어날 것 같지만 평균적으로 보면 처음 위치에서 계속 멀어집니다.
- 브라운 운동은 실제 주식의 예측 및 옵션가격 선정에도 쓰이고 있습니다.
- 인생에서도 지금 당장은 뭘 하는지 모르겠지만 아등바등 무언가 하다 보면, 처음보다는 더 멀리 가 있을 것입니다.
반응형
'잡담' 카테고리의 다른 글
| 쉽고 읽기 편한 글이 무조건 답은 아니다 (2) | 2024.03.12 |
|---|---|
| 벡터와 스칼라 - 기본 개념과 연산 (1) | 2023.10.21 |
| 존재하지 않는 수 - 허수 i 의 정의와 쓰임새 (1) | 2023.09.24 |
| 복잡한 경우의수를 풀때 - 몬테카를로(monte carlo) 방법 (0) | 2023.09.24 |
| 일본 후쿠시마 오염수 방류 관련 과학 지식 정리 (1) | 2023.08.29 |





