| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 프리다이빙
- 사진
- 닉슬립
- 3급공채
- 빅테크
- 반도체기초
- ai서버
- 직장인
- 책
- 수학#통계#몬테카를로#montecarlo#확률#과학
- MOSFET
- 프리다이빙입문
- 삼성전자
- 프리다이버
- 반도체란
- 파이썬
- 더머니북
- 자카리아
- 노마드투자자
- 취미
- freediving
- w를찾아서
- 반도체
- 입주전시공
- 일본#후쿠시마#오염수#방류#방사선#방사능#오염#피폭#발암물질#해산물#논란#뉴스
- 반도체 #tsmc #일본반도체정책 #대만일본협력 #기술격차 #문화충돌 #경제안보 #공급망 #국제협력 #산업정책
- the money book
- 독서
- brownian
- 트랜지스터
Archives
- Today
- Total
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 프리다이빙
- 사진
- 닉슬립
- 3급공채
- 빅테크
- 반도체기초
- ai서버
- 직장인
- 책
- 수학#통계#몬테카를로#montecarlo#확률#과학
- MOSFET
- 프리다이빙입문
- 삼성전자
- 프리다이버
- 반도체란
- 파이썬
- 더머니북
- 자카리아
- 노마드투자자
- 취미
- freediving
- w를찾아서
- 반도체
- 입주전시공
- 일본#후쿠시마#오염수#방류#방사선#방사능#오염#피폭#발암물질#해산물#논란#뉴스
- 반도체 #tsmc #일본반도체정책 #대만일본협력 #기술격차 #문화충돌 #경제안보 #공급망 #국제협력 #산업정책
- the money book
- 독서
- brownian
- 트랜지스터
Archives
- Today
- Total
sean's archive
존재하지 않는 수 - 허수 i 의 정의와 쓰임새 본문
반응형

1.허수
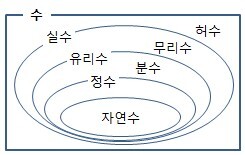
- 세상에는 여러 숫자가 있습니다. 손으로 셀 수 있는 숫자인 자연수(1, 2, 3, ...) 부터 시작해서 분수(1/3), 정수, 유리수, 무리수 등등 수에는 분류가 있습니다. 숫자가 길건 짧건 복잡하건간에 이런 숫자들은 모두 실제로 존재합니다. 그래서 실제로 존재하는 수인 '실수' 라고 이름이 붙어 있습니다.
- 숫자들을 종류별로 나눠놓은 기준을 수 체계(number system)라고 합니다.
- 잠깐 다른 얘기를 해봅시다. 제곱근(square root) 이라는 정의가 있습니다. 2를 두번 곱하면 4 입니다. 2는 4의 제곱근 입니다. (2 x 2 = 4) 3을 두번 곱하면 9 입니다. 3은 9의 제곱근 입니다. (3 x 3 = 9) 그렇다면 2의 제곱근은 무엇일까요? (? x ? = 2) 답은 1.4142... 입니다.
- 다시 원래 주제로 돌아와서 수 체계 얘기를 해보겠습니다. 수 체계를 보면 이상한 분류가 하나 있습니다. 바로 '허수' 입니다. 존재하지 않는 숫자 라는 뜻이죠. 두번 곱해서 -1 이 되는 숫자 입니다.
- 어떤 숫자도 두번 곱해서 음수가 될 수는 없습니다. 그래서 이를 허상의 수 (imaginary number) 인 '허수' 라고 합니다. 간단하게 i 로 표시합니다. (공학계열에서는 j 로 쓰는 경우도 많음)
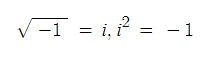
2. 독특한 성질
- 허수는 다른 수들과 더하고 빼고 곱하고 나누기가 가능합니다. 1+i 라는 숫자고 있고 2-i 라는 숫자도 있습니다.
- i 를 계속 곱했을 때 나타나는 규칙성이 있습니다.
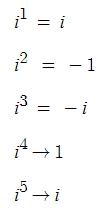
3. 복소수
- 실수와 허수를 더하면 복소수가 됩니다. 복소수는 실수부분과 허수부분으로 나눠볼 수 있습니다. 3+4i 라는 숫자가 있습니다. 이 숫자의 실수 부분은 3 이고 허수 부분은 4 입니다.
- 복소수끼리 더하거나 뺄수 있고, 그때 실수부분끼리 더하고 허수부분끼리 더하면 됩니다.

- 이 복소수도 절댓값 (absolute value) 를 가지고 있습니다. 3+4i 의 절댓값은 무엇일까요? 답은 5 입니다.
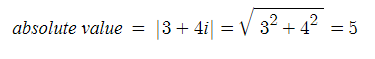
4. 쓰임새
- 허수 이녀석 어디에 쓰는걸까요? 생각보다 과학과 공학 분야에서 굉장히 많은 곳에서 쓰이고 있습니다.
- 진동하고 있는 물체가 있다고 해봅시다. 이걸 어떻게 표현해야 할까요?
- 진동하는 상태라고 하니 실생활에서 감이 잘 안오실 수 있습니다. 예를 들면, 우리가 사용하고 있는 전기는 220V의 교류(AC)입니다. 전압이 위아래로 계속 움직이고 있죠.
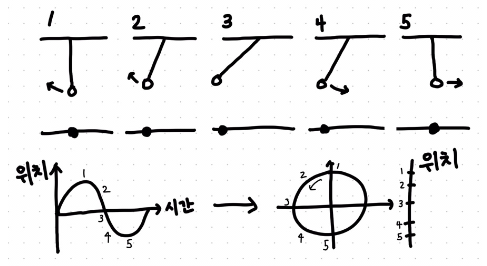
- 이 친구의 움직임은 우리가 중학교때 배웠던 삼각함수를 사용해서 구할 수 있습니다. 대표적으로는 사인(sine) 함수가 있습니다.
- 깊게 들어가지는 않고, 간단하게 사인 함수는 똑같은 모양이 반복되는 함수이고, 이런 사인함수를 복소수를 사용해서 표현할 수 있습니다.
- 왜 복소수를 사용하냐면, 이 표현법을 썼을 때 더하고 곱하고 나누는데 훨씬 많이 편리하기 때문입니다.
- 즉 허수를 사용하면 진동, 파동 등 주기적인 움직임을 가지는 물체의 운동을 쉽게 수학적으로 다룰 수 맀습니다. 물리학과 공학에서 많이 쓰고 있습니다.
5. 결론
- 허수는 두번 곱해서 -1 이 되는 수를 뜻합니다. 간단하게 i 라고 표시합니다.
- 허수를 사용한 숫자인 복소수는 진동, 파동 등 흔들리는 움직임을 표현하는데 사용되고 있으며, 물리학과 공학에서 널리 사용되고 있습니다.
- 실제 숫자가 아닌데 실제 세상에서 활발하게 사용되고 있다는 점이 참 재미있습니다.
- 실제 세상에 나타나는 부분은 숫자의 실수부 입니다. 하지만 안쪽에 있는 허수부에도 참 많은 정보가 담겨있습니다. 사람도 비슷한 것 같습니다. 겉으로 드러나는 부분만 보기보다는 내면도 파악하는게 중요한 것 같네요.
6. 복소 평면 (심화편)
- 일반적으로 복소수를 z 라는 알파벳으로 사용합니다. a+bi 를 z 라고 했을때, 실수부 a 는 Re(z) 로, 허수부 b 는 Im(z) 로 씁니다. Re(z) 를 x 축에, Im(z) 를 y 축에 표현할 수 있습니다. 이를 복소 평면이라고 합니다. 그러면 자연스럽게 복소수의 반지름인 r 값과 각도 theta 를 정의할 수 있습니다. 물론 r은 실수입니다.
- z = r[cos(theta) + i sin(theta)] 의 형태로 쓸수 있습니다. 그런데 여기서 r 내부의 표현을 또 exp(i*theta) 로 줄여쓸 수 있습니다. (오일러 공식) 한 복소수를 r*exp(i*theta) 의 극좌표계 형식으로 나타낼 수 있다는 것 입니다. 이렇게 쓰면 고차 방정식의 풀이가 생각보다 간단해 집니다. 예를 들면 x^5 = 1 을 푼다고 해봅시다. 이거 일반적인 다항 방정식의 풀이로는 풀 수가 없습니다. 그런데 극좌표계의 형태를 가져오면 문제가 쉬워집니다.
- 극좌표계의 형식을 가져오면, 두 복소수의 곱셈, 나눗셈, 미분, 적분 등이 쉬워집니다.
- theta = 2n*pi/5 가 답으로 나옵니다. 즉 복소평면에서 360도를 5등분해서 좌표를 찍으면, 그때의 복소수들이 이 방정식의 해가 되는 것 입니다.
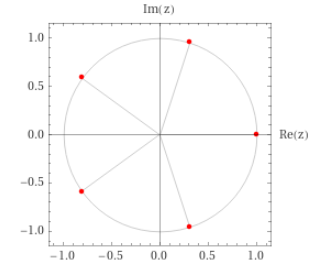
- Periodic 운동을 하고 있는 물체가 있을때, 그 물체의 운동을 복소수의 real 값으로 정의할 수 있습니다. 그리고 물체의 주기 T 도 당연히 복소수에 반영되어야 하겠죠. 주기적인 운동을 한번 반복하는데 걸리는 시간을 T (Period) 라고 하고, 1초에 몇번 반복되는지를 f (frequency) 라고 합니다. f 는 T 의 역수로 정의합니다. 간단하게 복소평면의 한 바퀴를 도는데 걸리는 시간이라고 생각하시면 됩니다. 또는 각속도 w 를 2*pi*f 로 정의해서 사용하기도 합니다.
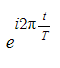
- 그래서 파동방정식을 풀때 2pi 가 계속 어디선가 꼬리표처럼 따라다닙니다.
반응형
'잡담' 카테고리의 다른 글
| 벡터와 스칼라 - 기본 개념과 연산 (1) | 2023.10.21 |
|---|---|
| 브라운 운동(Brownian motion) - 공기 중 먼지에서부터 주식까지 (1) | 2023.09.25 |
| 복잡한 경우의수를 풀때 - 몬테카를로(monte carlo) 방법 (0) | 2023.09.24 |
| 일본 후쿠시마 오염수 방류 관련 과학 지식 정리 (1) | 2023.08.29 |
| 영화 '오펜하이머' 관람 후기 - 미리 알아두면 좋은 정보 (0) | 2023.08.27 |





