| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- MOSFET
- 파이썬
- 자카리아
- 수학#통계#몬테카를로#montecarlo#확률#과학
- 반도체기초
- 입주전시공
- 트랜지스터
- 반도체 #tsmc #일본반도체정책 #대만일본협력 #기술격차 #문화충돌 #경제안보 #공급망 #국제협력 #산업정책
- 삼성전자
- 일본#후쿠시마#오염수#방류#방사선#방사능#오염#피폭#발암물질#해산물#논란#뉴스
- 사진
- freediving
- 프리다이빙
- 프리다이버
- 닉슬립
- 반도체
- 직장인
- 3급공채
- 책
- brownian
- 취미
- 노마드투자자
- the money book
- 더머니북
- 빅테크
- ai서버
- 프리다이빙입문
- w를찾아서
- 독서
- 반도체란
- Today
- Total
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- MOSFET
- 파이썬
- 자카리아
- 수학#통계#몬테카를로#montecarlo#확률#과학
- 반도체기초
- 입주전시공
- 트랜지스터
- 반도체 #tsmc #일본반도체정책 #대만일본협력 #기술격차 #문화충돌 #경제안보 #공급망 #국제협력 #산업정책
- 삼성전자
- 일본#후쿠시마#오염수#방류#방사선#방사능#오염#피폭#발암물질#해산물#논란#뉴스
- 사진
- freediving
- 프리다이빙
- 프리다이버
- 닉슬립
- 반도체
- 직장인
- 3급공채
- 책
- brownian
- 취미
- 노마드투자자
- the money book
- 더머니북
- 빅테크
- ai서버
- 프리다이빙입문
- w를찾아서
- 독서
- 반도체란
- Today
- Total
sean's archive
벡터와 스칼라 - 기본 개념과 연산 본문
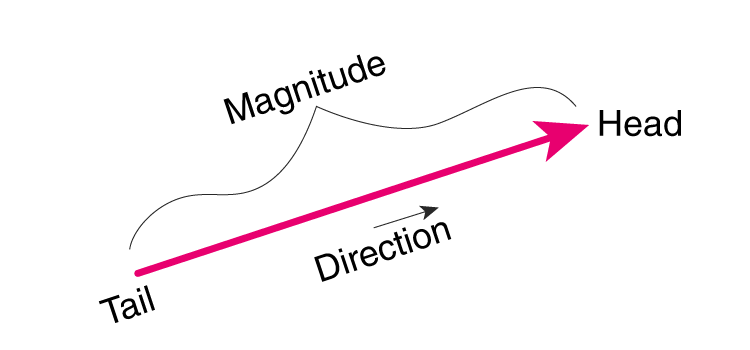
1. 벡터와 스칼라
세상의 물리량은 크게 두 가가지로 나눌 수 있습니다. 벡터와 스칼라 입니다. 스칼라는 크기만 가지고 있는 물리량을 뜻합니다. 예를 들면 몸무게가 40kg 라 가벼운 편이다, 온도가 30 도라 따뜻하다, 소리가 너무 크다 등등의 표현을 할때 사용되는 것이 스칼라 입니다.
벡터는 크기와 방향을 가지고 있는 물리량을 뜻합니다. 차가지고 부산 방향으로 시속 100km/h 으로 내려가고 있어 라던가, 타자가 포수에게 시속 150km/h 의 공을 던졌다던가 할때 이런 움직임을 벡터를 사용해서 표현합니다.
2. 벡터의 표현법
벡터는 간단하게 화살표로 표현합니다. 시작점과 끝점만 있으면 됩니다. 어디서부터 시작하던 상관 없습니다.
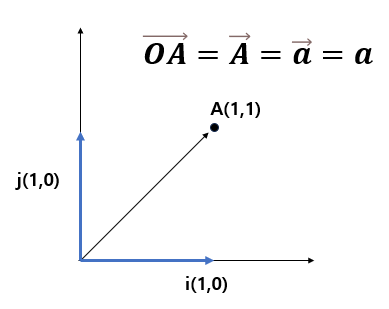
다만 이런 벡터를 표현하는 방식은 있어야 겠죠? 보통 원점을 기준으로 시작해서 끝나는 점을 벡터로 표현합니다. O (원점) 에서 시작해서 A (1,1)로 가면 이 벡터는 OA 로 표시하고 (1,1) 으로 나타내기도 합니다. 또는 대문자 A 를 굵게 쓰기도 하고, 소문자 a 를 굵게 쓰기도 합니다. 또는 벡터 표현법으로 a = 1i + 1j 로 쓰기도 합니다. i ,j 는 방향의 기본 단위로, i=(1,0), j=(0,1) 이며 이를 단위 벡터라고 합니다.표기법 자체는 다양합니다.
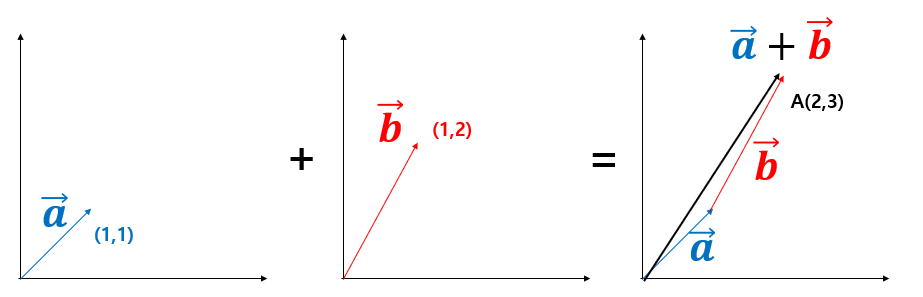
3. 벡터의 덧셈, 뺄셈, 곱셈
이런 벡터도 더하고 빼는 방법이 있습니다.예를 들어봅시다. a = (1,1) , b = (1,2) 라고 한다면 a+b 는 어떻게 구할까요? 두 화살표를 연달아서 그리면 됩니다. 좌표를 표현해서 사용한다면 (1,1) + (1,2) = (2,3) 으로 간단한 덧셈으로 두 벡터의 합을 구할 수 있습니다.
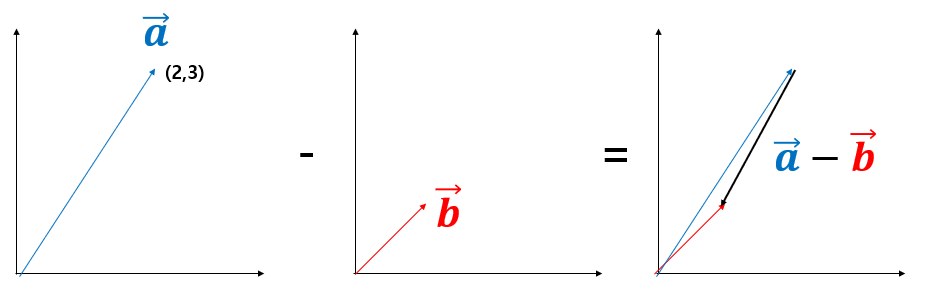
뺄셈은 직관적이지 않을 수 있습니다. a= (1,1) , c=(2,3) 이라고 합시다. 그럼 c 의 끝에서 a의 끝으로 연결한 게 c-a 입니다. 좌표로 표현하면, (2,3) - (1,1) = (1,2) 이니 간단합니다. 다만 와닿지 않을수도 있는데, 이는 반대 방향의 벡터를 더해준다고 생각해보면(c 와 -a 를 더한다) 조금 낫습니다.
숫자와의 (스칼라) 곱셈과 나눗셈은 매우 쉽습니다. 2 * a 는 단순하게 화살표를 두 배로 길게 늘린거고, a/2 는 a 를 반으로 줄인 겁니다. 좌표에 단순하게 곱하기와 나누기를 해주면 됩니다.
크기와 방향이 있는 모든것을 벡터로 표현할 수 있습니다만 주로 사용되는 표현법이 있습니다. 대표적으로는 물체의 위치를 나타내는 위치 벡터가 있습니다. position 의 약자로 p 로 쓰기도 하고, 일반적으로 좌표계에서 쓰는 x를 사용하기도 합니다.
4. 벡터의 사용처
x 가 시간에 따라 변하는 양을 속도 v (velocity) 라고 하고, v 가 시간에 따라 변하는 양을 가속도 a (acceleration)라고 합니다. 속도와 가속도도 벡터로 주로 사용합니다.
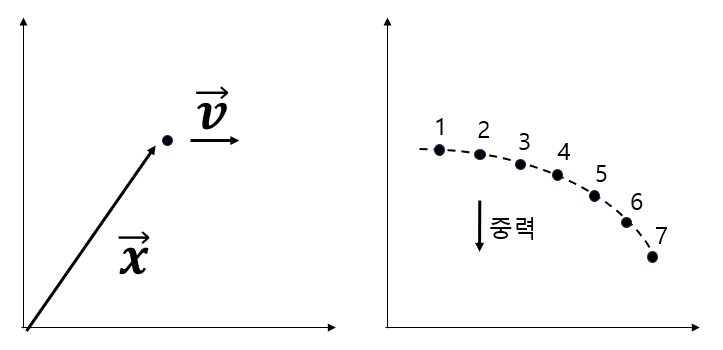
그리고 물체에 가하는 힘도 벡터로 표현합니다. 주로 F (Force) 로 사용을 합니다. 물체에 힘이 가해짐으로서 x 가 변하고 v 와 a 가 생기는거죠. 물리학의 가장 기본적인 식인 F=ma 가 나오지만, 여기서는 자세하게 다루지는 않겠습니다.
갑자기 왜 물리 얘기가 나오는지 궁금할 수도 있습니다. 네 사실 이런 표현법들은 대부분 물리학과 관련이 있거든요. 공을 수평으로 던지는 상황을 생각해봅시다. 그런데 중력은 항상 수직 방향으로 작용합니다. 그러니 공이 점점 떨어지지요. 그런데 중력이 공을 수평 방향으로 더 빠르게 하지는 않습니다. 즉 힘과 속도의 방향에 따라서 미치는 영향력이 다르다는 것이지요.
5. 내적 (Inner product)
한 벡터가 다른 벡터에 주는 영향을 어떻게 알 수 있을까요? 그때 내적이라는 계산법을 사용합니다. 내적은 (dot product 또는 inner product) 라고하는데, a dot b 로 표시합니다. a 와 b 의 크기에 두 벡터가 이루는 각도의 코사인(cos) 값을 곱해서 구합니다. |a|*|b|*cos(theta). 그리고 이 값은 스칼라 입니다.
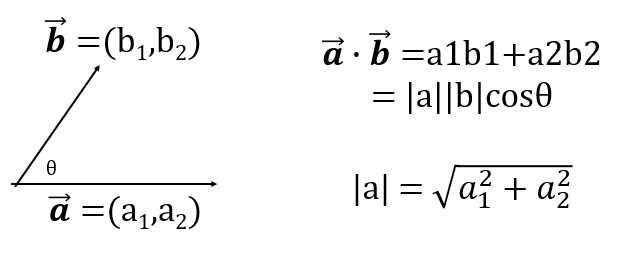
이는 좌표로도 간단하게 표현할 수 있는데, 단순하게 두 벡터의 좌표를 서로곱하면 됩니다. a 를 (a1,a2), b 를 (b1,b2) 라고하면, a dot b 는 a1*b1 + a2*b2 이고 이 값이 |a|*|b|*cos(theta) 와 동일합니다. (놀랍게도)
6. 외적 (cross product)
모든 크기와 방향을 가지는 양을 벡터라고 했었습니다. 그러면 회전하는 물체도 분명히 회전 방향과 크기를 가지고 있는데 이걸 어떻게 표현할까요? 애매합니다. 그런데 이를 정의한 방법이 있습니다. 반시계방향으로 돌때 이를 위쪽 벡터로, 시계 방향으로 돌때 이를 아래쪽 벡터로 표시합니다.
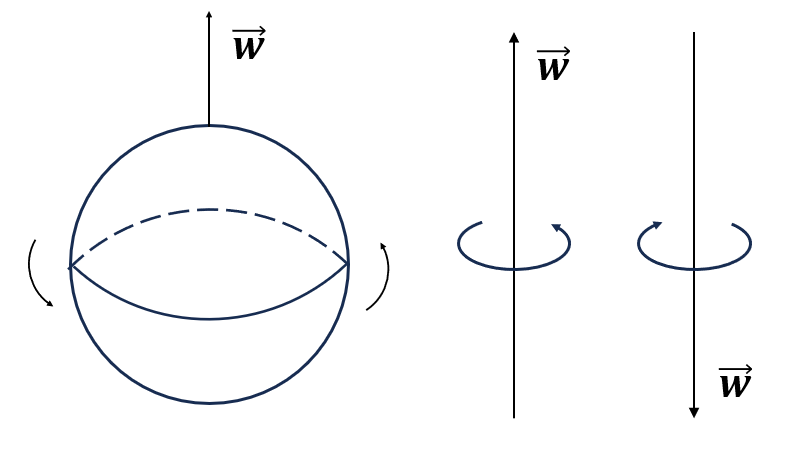
물체에 힘을 줬을때, 물체의 속도가 바뀌는 것을 내적으로 구했었습니다. 하지만 모든 물체는 속도 뿐 아니라 회전도 하죠. 물체를 돌리는 힘을 토크(torque) 라고 하는데, 이 토크를 구할때 사용하는 방법이 외적 (cross product) 입니다. a x b 로 표현합니다.
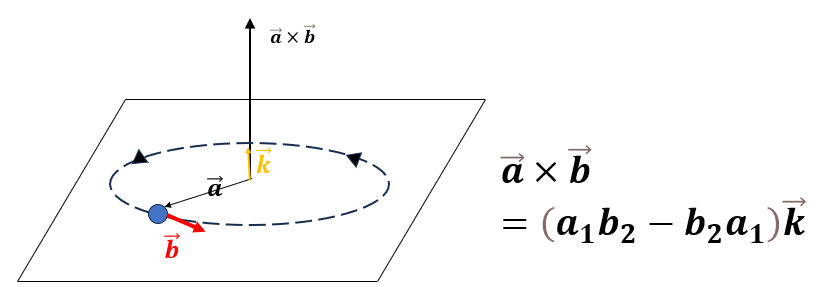
a 에 고정되어 있는 물체를 b 의 힘으로 돌린다고 가정해봅시다. 그러면 이때 시계 반대방향으로 힘을 주면, 회전 방향은 반시계 방향으로 도니까 토크 벡터는 위쪽입니다. 네, 내적과 다르게 외적의 결과물은 벡터 입니다.그것도 기존에 아에 존재하지 않았던 방향이요. (a1, a2) x (b1, b2) = |a|*|b|*sin(theta) 이고, a x b 의 좌표 표현법으로는 (a1*b2 - b1*a2) 의 위쪽 방향 벡터 입니다.
7. 마무리
벡터의 정의 및 간단한 연산 방법에 대해서 알아보았습니다. 이과에서는 이 벡터를 수도 없이 다루고 곱하고 더하고 빼고 내적하고 외적하고 합니다. 앞으로 쓸 글을 생각해서, 한번쯤은 언급하고 넘어가야 겠다고 생각했는데요. 고등학생 시절에 벡터때문에 수2 에서 조금 힘들었던 기억이 납니다.
'잡담' 카테고리의 다른 글
| 좋은 멘토링과 그 성공조건에 대하여 (0) | 2024.08.10 |
|---|---|
| 쉽고 읽기 편한 글이 무조건 답은 아니다 (2) | 2024.03.12 |
| 브라운 운동(Brownian motion) - 공기 중 먼지에서부터 주식까지 (1) | 2023.09.25 |
| 존재하지 않는 수 - 허수 i 의 정의와 쓰임새 (1) | 2023.09.24 |
| 복잡한 경우의수를 풀때 - 몬테카를로(monte carlo) 방법 (0) | 2023.09.24 |




